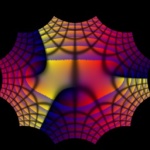
One of my oldest images, obtained by actually reverse-mapping an existing image using the Math Map plugin for Gimp. It seems to be a polynomial with three simple zeros.
|
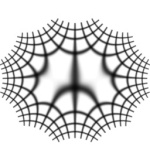
Same polynomial, same technique, but simple source image.
|
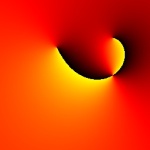
Also and old picture, this one is a rational function with two simple zeros and one double pole, graph with argument only. It is still one of my favorite images because of its simplicity, although it would probably benefit from some antialiasing.
|
 |

Polynomial (z2 + 1)(z−1)2. You can se the two simple zeros at ±i, and the double zero at 1.
|
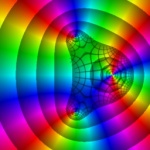
The same polynomial, using different way to display modulus, and with Re-Im grid in the center.
|
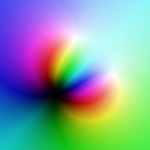
A rational function with two simple zeros and a double pole.
|
 |
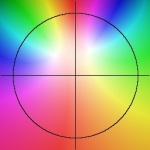
A Blaschke product with two factors.
|
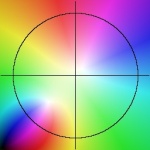
Another Blaschke product.
|
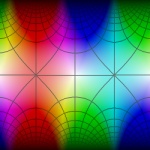
sin(z)
|
 |

(z2-1)/(z2+1). It has simple zeros at ±1 and simple poles at ±i.
|

The same rational function, this time the argument only.
|

The same rational function, zoomed out a bit.
|
 |

The same rational function, argument only, displayed with a gradient instead of the hue.
|
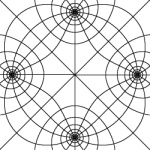
The same rational function, a reverse image of a polar grid.
|
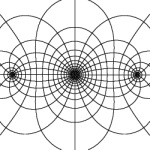
The same technique, this time for the function (z2-1)/z2.
|
 |
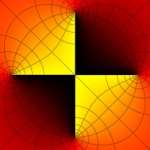
(z2-1)/(z2+1) again, this time the gradient is overlayed with a polar grid.
|

The same function, with gray bands indicating modulus.
|

The same function, argument only, this time with different gradient.
|
 |

The same function, polar \"checkerboard\"
|

The same function, regular (Re-Im) checkerboard.
|

Double zeros at ±1, triple poles at ±i.
|
 |

Same function, argument only, with gradient repeating twice for argument between 0 and 2π.
|

The same picture with bands of gray indicating the modulus.
|

The same function, zoomed out.
|
 |

The same function, zoomed out, argument only.
|
























