 |
A VV-singularity
A function f defined in the upper half plane has a VV-singularity at a point a at the real line if there exist two angles V1 and V2 in the upper half plane, with vertices at a, such that the set of accumulation points at a of f restricted to V1 is different from the the set of accumulation points at a of f restricted to V2
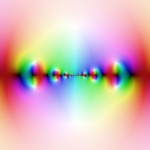
A function analytic in the upper
half plane that has a VV-singularity at the origin. It is based
on S. V .Kolesnikov: On Singular Boundary Points of Analytic
Functions, Matematiceskie Zametki, Vol 28, No 6, 1980. This is a very simple
case with only one singular point.
|
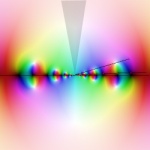
The same picture with some explanatory drawing on it. You can see
the zeros approaching the singularity in straight lines. You can see the Stoltz
angle close to the imaginary axis. The values inside this angle are all close
to 0 (low saturation). Finally, you can see a ray very close to the real axis, that passes close
to some singularities and therefore contains points arbitrarily close to the
origin where f has
very high modulus. It may be even more
clear if you look what happens with the argument. The angle contains very small
part of the spectrum, while both rays on the picture go through all the colors
of the rainbow over and over again
|

The same function, only larger and slightly better picture.
|
 |

A very similar function, except in this case 0 is not a point
of porosity of the set I used to define the function, and the function does not
have VV-singularity at 0. (The first function uses the set {1/2n; n ∈ N}
∪ {-1/2n; n ∈ N} ∪ {0}, which is porous at 0. The second uses set
{1/n; n ∈ Z}∪ {0}, which is not).
|

For comparison, the two functions are combined in the same picture. In the upper half plane, the function does not have a VV-singularity at 0, while the function in the lower half plane does.
|
|
 |




