We're trying to optimize and stablize a Colpitts oscillator so that we can measure electric and magnetic properties of materials. The basic circuit is shown below.
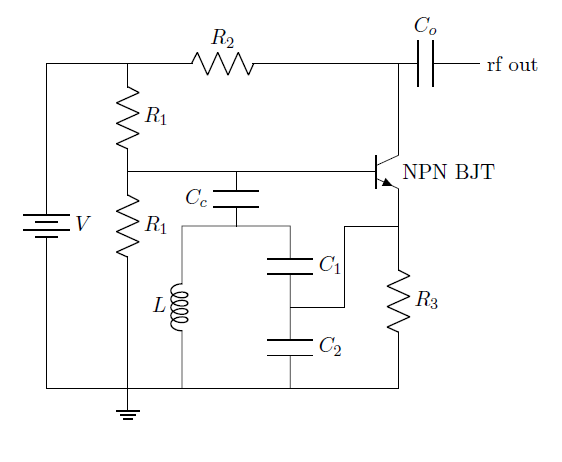
The design and function of a Colpitts oscillator can be found in many textbooks on basic electronics and online. The important part for our work is that the circuit produces a radio-frequency signal of a few MHz. The particular frequency depends on the values of the inductance, L and the two capacitors C1 and C2. There is some weak dependence on the base-emitter capacitance in the transistor, but for many applications this is ignorable. It turns out this is not the case for us. More on that later. We refer to the frequency of oscillation as the resonant frequency of the circuit.
If we put some material inside the inductor (call this material the "sample"), the inductance will change. We can observe and record that change by seeing the resonant frequency change. If we are able to vary the temperature of the smaple inside the inductor somehow, the properties of the sample will very likely change. This can lead to an additional change in the resonant frequency. Hence, we can, in principle, monitor changes in sample properties by measuring the changes in the resonant frequency of the oscillator. A problem is that if the temperature of the rest of the circuit changes, we'll see a frequency drift due to that. In addition, if the voltage we supply (the bias voltage) changes, the resonant frequency will change. We also have to cope with the fact that if the objects near the circuit move or change, that will change the resonant frequency.
The reason we have to worry about all of these effects is we want to observe very small changes in material properties. How small? As small as we possibly can. Since our direct measurement is the resonant frequency, we need it to be as stable as possible when the sample temperature is held constant. We must bring our "noise floor" down as low as possible. There are similar techniques (notably the tunnel diode resonator or TDR) that, under best case conditions, resonate at about 15 MHz with a stability of 0.01 Hz. That is, the frequency could be 14,763,489.03 Hz and the experimenter would know a change to 14,763,489.06 Hz was due to the sample property change. This is stability to 1 part per billion. The Colpitts oscillator is unlikely to achieve this level of stability. Still, every improvement we make is that much nicer.
Still, we have been able to get a circuit resonating at about 20 MHz stable to 1 Hz for a few hours. We did not try any special or extensive shielding, nor did we use a particularly stable voltage source. What mattered most was keeping the temperature stable. The 1 Hz stability came from a passive temperature stabilization at less than room temperature. This is where we start our work.
What we need to do
- Construct a circuit on a small stage. This will allow us to mount the circuit to an aluminum block so we can provide some active temperature control.
- Construct a very stable voltage source. We have something based on a REF102 integrated circuit with an opamp output buffer. There is a little work that needs done to make this better.
- Construct a mount so we can place the circuit/aluminum block on a closed cycle refrigerator capable of cooling to 173 K.
- 22 Nov 2024: We did not accomplish a lot this week, and that's okay. The circuit analysis is still proceeding. As I've indicated, my background is not electrical engineering. I have little experience analyzing circuits where we need to do tranformations beyond simple series/parallel combinations. Nor am I practiced with finding complex impedances and then using those to unravel resonance conditions. I can build circuits from diagrams, and I can design simple(ish) circuits using passive and basic active elements. Having Trista walk me through her understanding is extremely valuable. That said, over the coming Thanksgiving break, I'll be finishing my analysis of the Colpitts oscillator with an eye toward comparing results the last week of classes.
- 15 Nov 2024: Trista has explained how to do delta-Y (Δ-Y) transformations in circuits. This was something I had seen before, but not spent any time on. This is necessary for us to make progress analyzing the oscillator. A delta configuration is where three branches are connected to one another, but the node between any pair of branches has an additional lead coming in. As a consequence the branches are neither in series nor in parallel. They make a triangle - hence the "delta" name. Although, the drawing is typically done with the delta pointing down, so maybe it should be called "nabla" (∇). There is a way to convert this structure to a "Y" shaped configuration by combining the elements into new, equivalent elements. By adding the node, you can start replacing bits using the usual series/parallel rules, or by using charge and energy conservation. This week we're each going to try to simplify the circuit and see what we get. I'll try to update the diagram to show how we reduce to a simpler circuit.
- 9 Nov 2024: We added some simple shielding in the form of an Altoids tin. The short-term noise dropped to about 1-3 Hz over a few minutes. There is a strong drift due to temperature variation. Our next experimental steps are to cool the circuit to 77 K or so, and maintain a constant low temperature. Trista is working on how to model the circuit with an eye toward determining the power dumped into the tank circuit. If we minimize this while keeping the oscillation alive we should eliminate harmonics.
- 1 Nov 2024: Yesterday Trista got her circuit functioning. Previous iterations used the common P2N2222A transistor. This is a general purpose small signal transistor. Trista's current circuit uses a KSP10BU radio-frequency transistor. The significant difference is the former has a unity gain frequency of 300 MHz and for the latter it is 650 MHz. The oscillation frequency she has is 13.4-ish MHz. I do not know enough about transistor specifics to speak about the gain rolloff with frequency, but I know that as the unity gain frequency increases the gain at our operating frequencies is more likely to be stable. Trista's circuit ran overnight and when I came in the morning it was stable and fluctuating at the 10 Hz level (part per million stability). This is very encouraging because we have done nothing to shield the circuit from noise nor to stabilize the circuit temperature. So, we can implement some shielding and (now that we have a decent Arduino based temperature controller) thermal control to improve the stability.
- 26 Oct 2024: Based on our understanding of how a transistor actually works, we are adjusting the elements R1 and R3. We're also going to try using two different resistors for the two R1's. This would mean making a new circuit diagram, but we're being lazy about that. The purpose of this is to change how much power is delivered to the tank circuit on each cycle. If we adjust Cc we can also adjust the power fedback to the transistor base.
Updated 24 November 2024